[백준] 1655 가운데를 말해요 파이썬 풀이
※ 사용언어 : 파이썬 ※
▼ 문제 링크 ▼
https://www.acmicpc.net/problem/1655
1655번: 가운데를 말해요
첫째 줄에는 수빈이가 외치는 정수의 개수 N이 주어진다. N은 1보다 크거나 같고, 100,000보다 작거나 같은 자연수이다. 그 다음 N줄에 걸쳐서 수빈이가 외치는 정수가 차례대로 주어진다. 정수는 -1
www.acmicpc.net
문제 설명
◇ 해당 문제를 풀기 위해서는 두 개의 heap이 필요하다.
◇ 두 heap의 이름을 각각 leftheap, rightheap이라고 칭한다고 가정하면,
➡ leftheap은 중간값보다 작은 수가 들어가고 rightheap에는 중간값보다 큰 수가 들어간다.
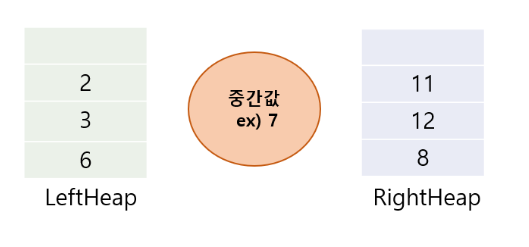
◇ 그림에서는 중간값을 따로 빼두었지만, 중간값도 결국에는 heap 안에 있어야 한다. 문제에서 '수빈이가 외친 수가 짝수개라면 중간에 있는 두 수 중에서 작은 수를 말해야한다' 라는 부분에서 우리는 중간값이 leftheap에 있어야 한다는 것을 알 수 있다. (leftheap에 작은 수가 들어갈 것이기 때문이다.)
➡ 결국 leftheap의 루트가 중간값이 되게 된다

문제 풀이 (With Python)
◇ 전체적인 풀이 과정은 다음과 같다.
| 1. leftheap과 rightheap의 길이가 같다면 (즉 두 heap에 들어있는 리스트 요소의 수가 같으면) 중간값의 기준이 되는 leftheap에 수를 넣는다. 반면, 길이가 같지 않다면 길이를 맞춰주기 위해 rightheap에 수를 넣는다. 2. 만약에 leftheap의 루트가 rightheap의 루트보다 크면 leftheap의 루트와 rightheap의 루트를 바꿔준다. why? leftheap은 중간값을 기준으로 작은 수가 들어가는 곳이다. 그런데 leftheap의 루트가 rightheap보다 크다면, 중간값보다 큰 수가 leftheap에 들어가있는 상황이기에 leftheap의 루트와 rightheap의 루트를 바꿔준다. |
◇ 코드
import sys
import heapq
N=int(sys.stdin.readline())
leftHeap=[]
rightHeap=[]
answer=[]
for i in range(N):
inputNum=int(sys.stdin.readline())
if len(leftHeap)==len(rightHeap):
heapq.heappush(leftHeap, (-inputNum, inputNum))
else:
heapq.heappush(rightHeap, (inputNum, inputNum))
if rightHeap and leftHeap[0][1] > rightHeap[0][0]:
min=heapq.heappop(rightHeap)[0]
max=heapq.heappop(leftHeap)[1]
heapq.heappush(leftHeap, (-min, min))
heapq.heappush(rightHeap, (max, max))
answer.append(leftHeap[0][1])
for j in answer:
print(j)
◇ 파이썬의 heapq는 기본적으로 최소 힙을 제공해준다. 하지만 최대 힙은 제공해주지 않기 때문에 heap에 숫자를 넣을 때 마이너스(-)를 취해 넣어준다. (최댓값에 마이너스를 붙이게 되면 최솟값이 되는 원리를 이용한 것이다.)
◇ leftheap이 최대힙인 이유는, leftheap에 들어간 수는 중간값보다 작은 수이다. 그 작은 수 중에서 가장 큰 값이 중간값이 되기 때문에 루트가 최댓값이 되는 최대 힙을 사용한다.
반대로 rightheap같은 경우 중간 값보다 큰 수 들이 들어가고 그 수 중에서 가장 작은 수가 중간 값 다음에 나와야 하기 때문에 가장 작은 수가 루트가 되는 최소 힙을 사용한다.
◇ heapq.heappop(rightHeap) 와 heapq.heappop(leftHeap)로 heap의 내용을 꺼내오게 되면 (max, max), (-min, min)의 꼴로 나오게 된다. 해당 튜플에서 불러와야하는 것은 max와 min이기 때문에 heapq.heappop(rightHeap) 뒤에 max 인덱스 값인 0과 heapq.heappop(leftHeap) 뒤에 min 인덱스 값인 1을 붙인다.
◇ leftheap의 루트값이 중간값이기 때문에 answer에는 leftheap의 루트 값을 넣는다.
해당 문자와 매우 유사한 문제가 있어 해당 문제를 이해한 뒤 복습 겸으로 풀어보시는 걸 추천드립니다.
백준 - 중앙값 구하기(2696)